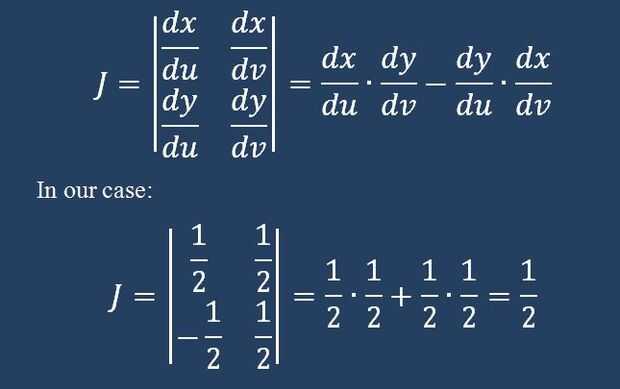El cambio de Variables de integrales dobles (3 / 10 paso)

Paso 3: Encontrar el determinante de Jacobian

El jacobiano es un determinante de una matriz que involucra X distinguido con respecto a usted y V, así como Y diferenciadas con respecto a u y V.  Para un integral con números variables, habrá números sustituciones y jacobiano será un determinante de nxn.  Esta es una razón que se requiere conocimientos previos.  Funciones multivariables, derivadas parciales y factores determinantes de la matriz se utilizan en este paso.  En nuestro caso dx/du = 1/2, dx y dv = 1/2, dy/du = -1/2 y dv/dy = 1/2.  Así, el determinante de Jacobian es 1/2.

Artículos Relacionados

Tutorial de Arduino Bundle.: Arduino Kit de experimentación:. (ARDX)

Tutorial de Arduino Bundle.: Arduino Kit de experimentación:. (ARDX)

¿Interesado en hacer proyectos aseados con un Arduino pero no está seguro de dónde empezar?Aquí es fácil de seguir guía acerca de cómo conectar y utilizar un conjunto de componentes electrónicos.(shameless plug)¿Interesados en hacer todo?Kits complet
Utilizando componentes de NXT con un Micro controlador

Utilizando componentes de NXT con un Micro controlador

esto es una guía para usar los motores y sensores de LEGO NXT con Parallax Basic Stamp II o BS2.  Sin embargo, en lugar de sólo proporcionar esquemas y ejemplos de código para el BS2, va a proporcionar alguna teoría sobre cómo funcionan los sensores
Movimiento activa la iluminación exterior

Movimiento activa la iluminación exterior

iluminación es uno de los aspectos más importantes de su hogar o negocio. Sino encender las luces y apagar todo el tiempo es un fastidio, sin dejar de mencionar la energía desperdiciado cuando, inevitablemente, se olvide de apagar por la noche. Por e
Reloj universal conveniente para invidentes

Reloj universal conveniente para invidentes

estaba googleando en busca de algún tipo de dispositivo podría hacer utilizando arduino y tropezó con eshop con dispositivos para invidentes. Lo que realmente me sorprendió fue el precio. Quiero decir-me doy cuenta de que tales dispositivos no son re
Sable de luz Darth Maul LED

Sable de luz Darth Maul LED

crear una barata pero efectiva doble terminó el sable de luz para una fiesta de disfraces de ciencia ficción.Cualquiera que haya visto Star Wars sabe Señor Kickarse 'Darth Maul'. Él era diferente, tenía un sable de luz que tenía una hoja en cada extr
Tirantes de señal de giro

Tirantes de señal de giro

Aquí es un enlace a un video de ellos!   http://youtu.be/b04B_yZ8EhYInspirado por el suéter de la señal de vuelta.  Sonaba muy bien, excepto no usar suéteres en calor del mediodía de verano, o en días fríos de invierno. Entrar en las ligas!He pensado
Lo básico de Mathcad

Lo básico de Mathcad

Mathcad es un programa de computadora para resolver los problemas de matemáticas simples y complejas; se puede considerarse como una calculadora con esteroides. Utiliza todo el mundo para calcular ecuaciones complejas en segundos, Mathcad es una pode
Distinguir caminando y corriendo con el aprender de máquina

Distinguir caminando y corriendo con el aprender de máquina

Mercado electrónico está lleno de dispositivos llamados podómetro y fitness tracker. Cuenta el número de pasos que ha tomado, la distancia ha cubierto, ya sea caminando o corriendo y montón de otras cosas. Preguntado, cómo estos dispositivos realizan
Hacer un molino CNC con un cortador láser

Hacer un molino CNC con un cortador láser

¿Por lo tanto, tienes un cortador del laser CNC pero quieres un molino CNC? Problema solucionado.Este proyecto es un pequeño molino CNC que se puede montar de comprado y laser-corte las piezas de alrededor de $800 sin máquinas de herramientas. (Si ti
Movimiento exterior Kit de la luz

Movimiento exterior Kit de la luz

Este proyecto requiere la comprensión de cómo leer un circuito esquemático. La Ardweeny tiene su propio incluidoinstrucciones y tendrá que armarse primero antes de se instala en el protoboard. La placa de circuito y relé se alojaran en una caja de pl
Tanque Control remoto

Tanque Control remoto

¿Que siempre quisiste a la unidad en torno a un tanque? Esto podría ser lo mejor. Con no mucho de la habilidad necesaria, cualquier persona puede construir este chasis de tanque. Entonces todo lo que tienes que hacer es personalizarlo para su uso, qu
Hacer Tic Tac Toe en Java

Hacer Tic Tac Toe en Java

este instructivo le guiará, paso a paso, por lo que Tic Tac Toe en Java! Esto no pretende ser un resumen del lenguaje Java, pero más de un ejemplo guiado. El primer paso será ir sobre algunos conceptos básicos para hacer el resto de la guía bajar sua
Cómo escribir un sencillo programa de C++

Cómo escribir un sencillo programa de C++

en este tutorial, aprenderás cómo escribir un programa en C++ lenguaje de programación. Esto irá sobre 10 pasos que explicarán un simple programa de C++. Los temas que cada paso en este tutorial se utilizan a menudo en programas de C++ más complejos.
LittleBits Arduino MacBook Air Blink bosquejo

LittleBits Arduino MacBook Air Blink bosquejo

¿Conoces Littlebits Arduino? Es super sencillo y recto hacia adelante para utilizar.Paso 1: Tire los módulos Littlebits del kit para el bosquejo de parpadear Se reúnen los componentes del proyectoBatería de 9V + CableEnergíaGráfico de barrasArduinoMa