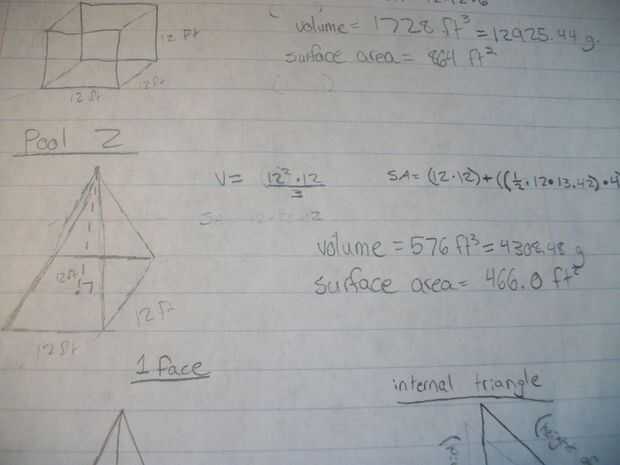La situación de la piscina (3 / 7 paso)

Paso 3: Cálculo de piscina 2

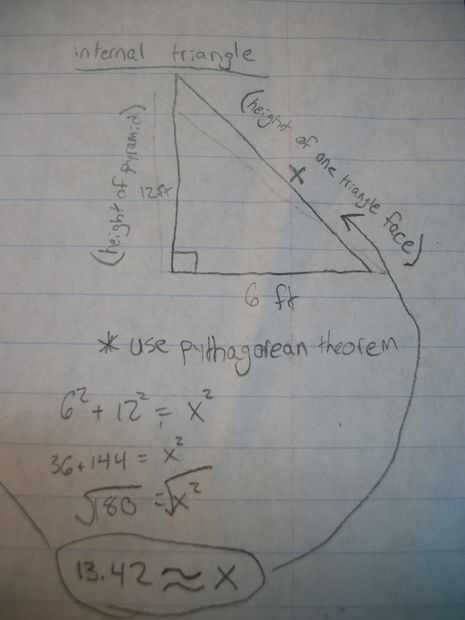
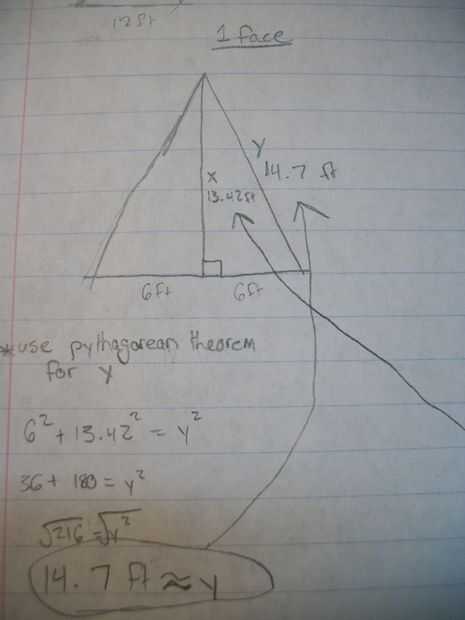
Puesto que el grupo 2 fue una pirámide, había más cálculos que necesita para hacer frente a la piscina 1.  Para encontrar el volumen, hicimos una tercera base cuadrada veces altura (1/3 * cuadrado 12 * 12).  En cuanto a la superficie, necesitábamos encontrar valores adicionales para encontrar la superficie.  Teníamos que encontrar la altura de una de las caras del triángulo.  Para ello, hemos creado un triángulo rectángulo con la altura (12 pies) como una de las patas y la mitad de la base (6 pies) como la otra pierna.  Desde allí, utilizamos el teorema de Pitágoras para encontrar la longitud de la hipotenusa (13,42 pies), que era también la altura de cada cara del triángulo de la pirámide.  Con esta información, podemos encontrar el área de un triángulo cara y multiplicarla por 4 para encontrar el área superficial de todo pero la base.  Para encontrar el área de la base, todo lo que tuvimos que hacer fue largo veces ancho.  Mediante la adición de la zona del triángulo de cuatro caras y el área de la base cuadrada, fuimos capaces de encontrar la superficie de la pirámide entera.  Nuestra ecuación de la superficie final parecía esto: (12*12)+((1/2*12*13.42)*4).